Existen tres formas:
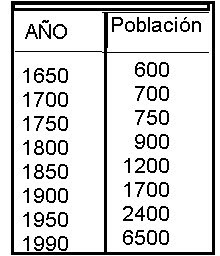
Aquí la variable independiente es el año y la variable dependiente es la población.
La variable (y) dependiente, población , depende de la variable (x) independiente, año.----> Población = F ( x)
2) Gráfica
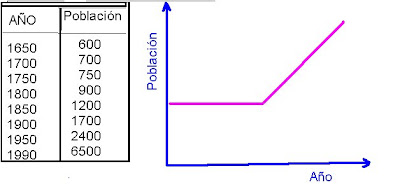
3) Fórmula
+%3D+y.bmp)
TIPOS DE FUNCIONES
FUNCIÓN INYECTIVA O UNO A UNO
- Mediante una tabla de datos
- Mediante un gráfico
- Mediante fórmulas

Aquí la variable independiente es el año y la variable dependiente es la población.
La variable (y) dependiente, población , depende de la variable (x) independiente, año.----> Población = F ( x)
2) Gráfica

3) Fórmula
+%3D+y.bmp)
TIPOS DE FUNCIONES
- Función inyectiva o 1 - 1
- Función epiyectiva o sobre
- Función biyectiva
- Función inversa
- Función compuesta
- Función de segundo grado
FUNCIÓN INYECTIVA O UNO A UNO
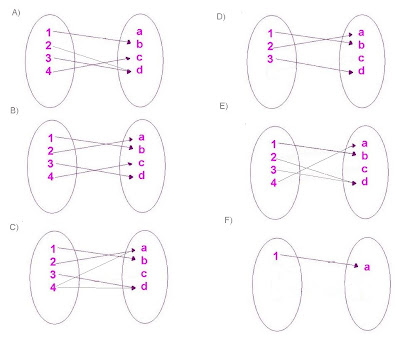
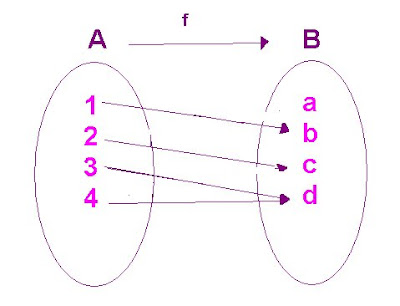
Una función f: A--> B se dice inyectiva o uno a uno si y sólo si elementos distintos en A le corresponden imágenes distintas en B.
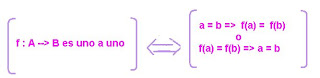 Veamos un ejemplo:
Veamos un ejemplo:
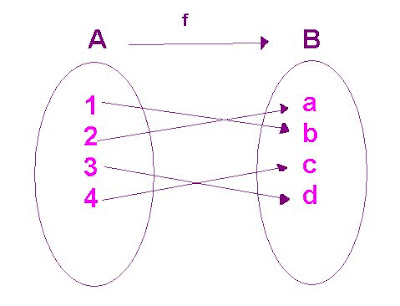
f es uno a uno, cada elemento de B es imagen de A.
De los siguientes ejemplos .¿Cuáles es(son) función(es) inyectiva o 1 a 1?. La respuesta entrégala en comentario(ubicado al final de la ficha)
 Veamos un ejemplo:
Veamos un ejemplo:
f es uno a uno, cada elemento de B es imagen de A.
De los siguientes ejemplos .¿Cuáles es(son) función(es) inyectiva o 1 a 1?. La respuesta entrégala en comentario(ubicado al final de la ficha)

FUNCIÓN EPIYECTIVA O SOBRE
Función compuesta o composiciones de funciones.
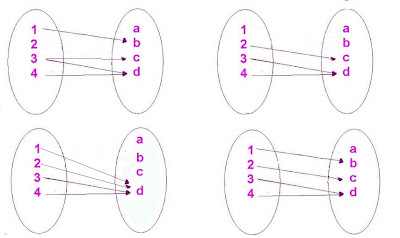
Una función f: A-->B se dice epiyectiva o sobre si y sólo si todo elemento de B es imagen de algún elemento de A
( f: A --> B es sobre ) <=> ( Rang f = B)
Veamos un ejemplo:
 Todo elemento de A debe tener a lo menos una imagen en B
Todo elemento de A debe tener a lo menos una imagen en B

De los siguientes ejemplos .¿Cuál(es) es(son) función(es) epiyectiva o sobre. La respuesta entrégala en comentario(ubicado al final de la ficha)
FUNCIÓN BIYECTIVA
A cada elemento de A le corresponde un único elemento de B.
( f: A --> B es sobre ) <=> ( Rang f = B)
Veamos un ejemplo:
 Todo elemento de A debe tener a lo menos una imagen en B
Todo elemento de A debe tener a lo menos una imagen en B
De los siguientes ejemplos .¿Cuál(es) es(son) función(es) epiyectiva o sobre. La respuesta entrégala en comentario(ubicado al final de la ficha)

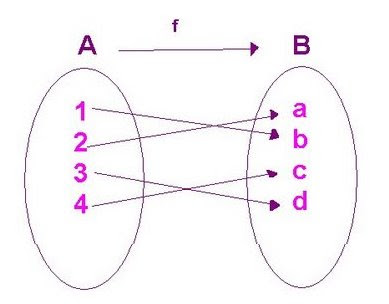
Una función f: A -- >B es biyectiva si y solo si es 1 - 1 y sobre.

A cada elemento de A le corresponde un único elemento de B.
Función compuesta o composiciones de funciones.
Dados dos funciones f : A--> B --> C queremos definir una nueva función desde x a z utilizando las funciones f y g. Tal función se denotará por g o f y se llama compuesta de f por g (o la composición) de f o g
Son tres funciones:
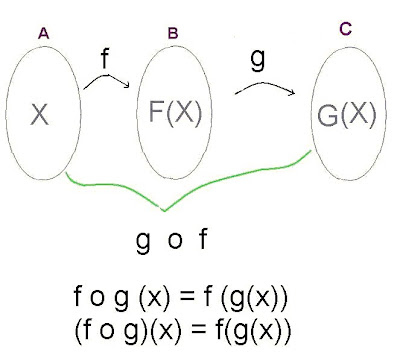
Se tiene que f(x) = 2x-2 y g(x) = x + 2; entonces
(f o g) (x)=
A) 2X
B) 2X - 2
C) 2X + 2
D) 2X + 4
E) 2X + 6
Solución:
f(x) = 2x-2 y g(x) = x + 2; entonces (f o g) (x)=
f(x +2) =
= 2 (x+2) - 2
= 2x + 4 - 2
= 2x + 2
(f o g) (x)= 2x + 2
Son tres funciones:

Se tiene que f(x) = 2x-2 y g(x) = x + 2; entonces
(f o g) (x)=
A) 2X
B) 2X - 2
C) 2X + 2
D) 2X + 4
E) 2X + 6
Solución:
f(x) = 2x-2 y g(x) = x + 2; entonces (f o g) (x)=
f(x +2) =
= 2 (x+2) - 2
= 2x + 4 - 2
= 2x + 2
(f o g) (x)= 2x + 2





No hay comentarios:
Publicar un comentario