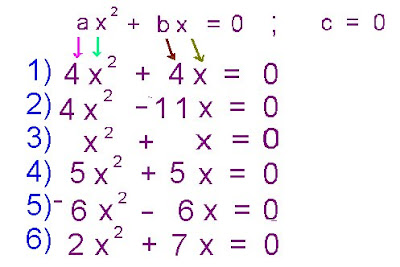Existen tres formas:
- Mediante una tabla de datos
- Mediante un gráfico
- Mediante fórmulas
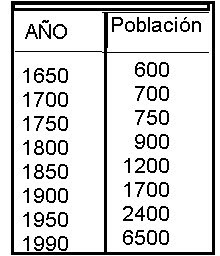
Aquí la variable independiente es el año y la variable dependiente es la población.
La variable (y) dependiente, población , depende de la variable (x) independiente, año.----> Población = F ( x)
2) Gráfica
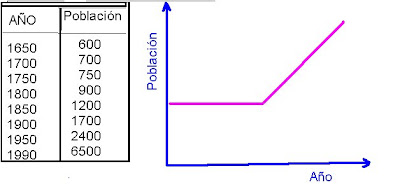
3) Fórmula
+%3D+y.bmp)
TIPOS DE FUNCIONES
- Función inyectiva o 1 - 1
- Función epiyectiva o sobre
- Función biyectiva
- Función inversa
- Función compuesta
- Función de segundo grado
FUNCIÓN INYECTIVA O UNO A UNO
Una función f: A--> B se dice inyectiva o uno a uno si y sólo si elementos distintos en A le corresponden imágenes distintas en B.
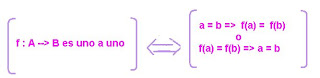 Veamos un ejemplo:
Veamos un ejemplo:
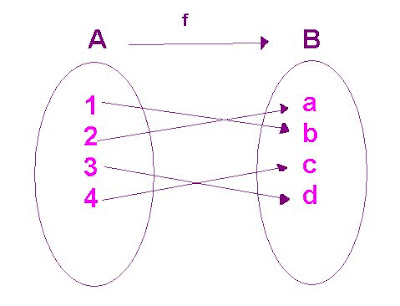
f es uno a uno, cada elemento de B es imagen de A.
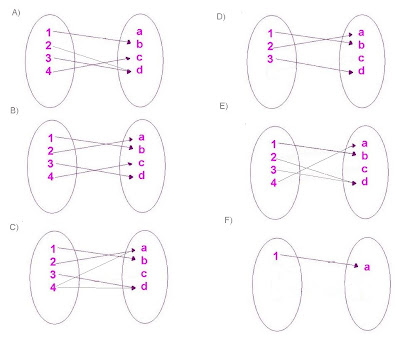
De los siguientes ejemplos .¿Cuáles es(son) función(es) inyectiva o 1 a 1?. La respuesta entrégala en comentario(ubicado al final de la ficha)
 Veamos un ejemplo:
Veamos un ejemplo:
f es uno a uno, cada elemento de B es imagen de A.
De los siguientes ejemplos .¿Cuáles es(son) función(es) inyectiva o 1 a 1?. La respuesta entrégala en comentario(ubicado al final de la ficha)

FUNCIÓN EPIYECTIVA O SOBRE
Función compuesta o composiciones de funciones.
Una función f: A-->B se dice epiyectiva o sobre si y sólo si todo elemento de B es imagen de algún elemento de A
( f: A --> B es sobre ) <=> ( Rang f = B)
Veamos un ejemplo:
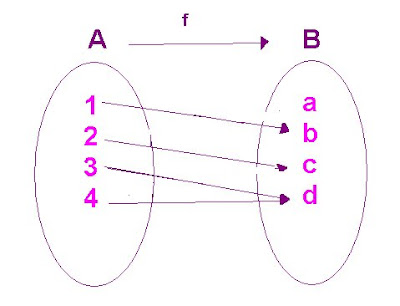 Todo elemento de A debe tener a lo menos una imagen en B
Todo elemento de A debe tener a lo menos una imagen en B

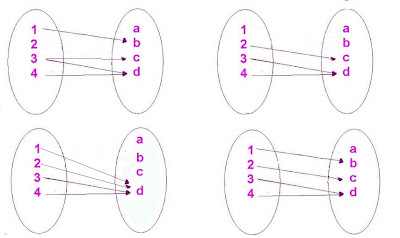
De los siguientes ejemplos .¿Cuál(es) es(son) función(es) epiyectiva o sobre. La respuesta entrégala en comentario(ubicado al final de la ficha)
FUNCIÓN BIYECTIVA
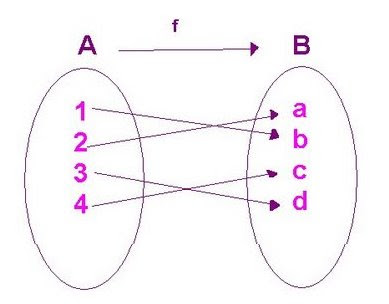
A cada elemento de A le corresponde un único elemento de B.
( f: A --> B es sobre ) <=> ( Rang f = B)
Veamos un ejemplo:
 Todo elemento de A debe tener a lo menos una imagen en B
Todo elemento de A debe tener a lo menos una imagen en B
De los siguientes ejemplos .¿Cuál(es) es(son) función(es) epiyectiva o sobre. La respuesta entrégala en comentario(ubicado al final de la ficha)

Una función f: A -- >B es biyectiva si y solo si es 1 - 1 y sobre.

A cada elemento de A le corresponde un único elemento de B.
Función compuesta o composiciones de funciones.
Dados dos funciones f : A--> B --> C queremos definir una nueva función desde x a z utilizando las funciones f y g. Tal función se denotará por g o f y se llama compuesta de f por g (o la composición) de f o g
Son tres funciones:
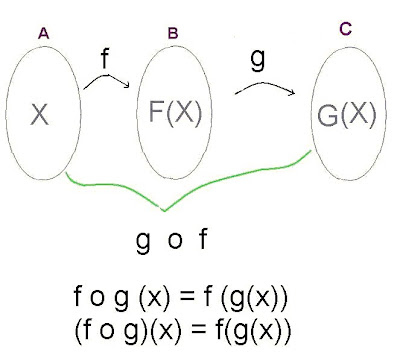
Se tiene que f(x) = 2x-2 y g(x) = x + 2; entonces
(f o g) (x)=
A) 2X
B) 2X - 2
C) 2X + 2
D) 2X + 4
E) 2X + 6
Solución:
f(x) = 2x-2 y g(x) = x + 2; entonces (f o g) (x)=
f(x +2) =
= 2 (x+2) - 2
= 2x + 4 - 2
= 2x + 2
(f o g) (x)= 2x + 2
Son tres funciones:

Se tiene que f(x) = 2x-2 y g(x) = x + 2; entonces
(f o g) (x)=
A) 2X
B) 2X - 2
C) 2X + 2
D) 2X + 4
E) 2X + 6
Solución:
f(x) = 2x-2 y g(x) = x + 2; entonces (f o g) (x)=
f(x +2) =
= 2 (x+2) - 2
= 2x + 4 - 2
= 2x + 2
(f o g) (x)= 2x + 2
Cuando se tiene la variable X, se tiene :
donde
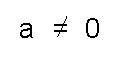 es decir tendrá dos soluciones el valor de x
es decir tendrá dos soluciones el valor de x
¿Qué son las raíces? Son las soluciones.
Clasificación de función de 2º grado o cuadrática:
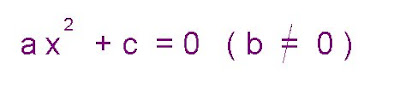
 Resuelve los siguientes ejercicios. La respuesta de las raíces encontradas ponlas en comentario ubicado al final de la ficha)
Resuelve los siguientes ejercicios. La respuesta de las raíces encontradas ponlas en comentario ubicado al final de la ficha)
 Resuelve los siguientes ejercicios. La respuesta de las raíces encontradas ponlas en comentario ubicado al final de la ficha)
Resuelve los siguientes ejercicios. La respuesta de las raíces encontradas ponlas en comentario ubicado al final de la ficha)
Resuelve los siguientes ejercicios. La respuesta de las raíces encontradas ponlas en comentario ubicado al final de la ficha)

donde
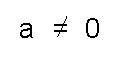 es decir tendrá dos soluciones el valor de x
es decir tendrá dos soluciones el valor de x¿Qué son las raíces? Son las soluciones.
Clasificación de función de 2º grado o cuadrática:
- Ecuación 2 º grado o cuadrática incompleta pura
- Ecuación 2 º grado o cuadrática incompleta particular.
- Ecuación 2 º grado o cuadrática completa particular
- Ecuación 2 º grado o cuadrática completa general
Ecuación 2 º grado o cuadrática incompleta pura
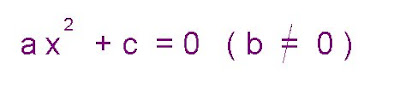
 Resuelve los siguientes ejercicios. La respuesta de las raíces encontradas ponlas en comentario ubicado al final de la ficha)
Resuelve los siguientes ejercicios. La respuesta de las raíces encontradas ponlas en comentario ubicado al final de la ficha) Resuelve los siguientes ejercicios. La respuesta de las raíces encontradas ponlas en comentario ubicado al final de la ficha)
Resuelve los siguientes ejercicios. La respuesta de las raíces encontradas ponlas en comentario ubicado al final de la ficha)Resuelve los siguientes ejercicios. La respuesta de las raíces encontradas ponlas en comentario ubicado al final de la ficha)