En un gráfico sagital, una relación es función si de todos los elementos del primer conjunto sale una sola flecha.
EJERCICIOS RESUELTOS
1) Sean A = {1, 2, 3} y B = {4, 5, 6}. Dadas las relaciones de A en B. Determinar cuáles son funciones.
a) R = {(1,4), (2,5), (3,6)}
b) R = {(1,4), (2,4). (3,4)}
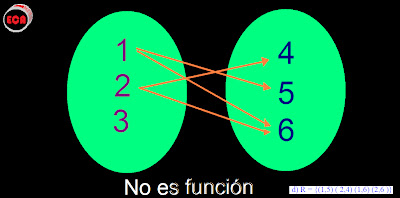
c) R = {(1,4), (1,5), (1,6), (2,4), (3,6)}
d) R = {(1,5), (2,4), (1,6), (2,6)}
e) R = {(1,6), (2,4), (3,6)}
SOLUCIÓN
a) R = {(1,4), (2,5), (3,6)}
a) R es función porque todos los elementos de A tienen una sola imagen en B.
b) R = {(1,4), (2,4), (3,4)}
b) R es función porque todos los elementos de A tienen una sola imagen en B, no importa que ésta sea la misma para todos.
- R = {(1,4), (1,5), (1,6), (2,4), (3,6)}
c) R no es función porque 1 є A tiene más de una imagen en B.
d) R = {(1,5), ( 2,4), (1,6), (2,6 )}
d) R no es función porque 3 є A no tiene imagen en B.
e) R = {(1,6) (2,4) (3,6)}
e) R es función porque todos los elementos de A tienen una única imagen en B.
2) Sean A = {1,3,5,7} y B = {2,4,6}. Determine si las siguientes relaciones de A en B son o no funciones. Justifique la respuesta.
a) R = {(1,2), (3,4), (5,6), (7,6)}
b) R = {(1,2), (3,4), (5,6)}
c) S = {(3,4), (5,6), (7,2), (7,4)}
d) S = {(1,4), ( 3,4), (5,4), (7,4 )}
e) T = {(7,6), (5,4), (3,2), (1,2)}
f) T = {(1,6), (3,4), (5,2), (5,4), (7,6)}
g) R = {(3,2), (3,4), (3,6)}
SOLUCIÓN
a) R = {(1,2), (3,4), (5,6), (7,6)}
a) R es función porque cada elemento de A tiene imagen única en B.
b) R = {(1,2), (3,4), (5,6)}
b) R no es función porque 7 є A no tiene imagen en B.
c) S = {(3,4), (5,6), (7,2), (7,4)}
c) S no es función porque 1 є A no tiene imagen en B y además 7 є A tiene más de una imagen.
d) S = {(1,4), ( 3,4), (5,4), (7,4 )}
d) S es función porque cada elemento de A tiene imagen única en B.
e) T = {(7,6), (5,4), (3,2), (1,2)}
e) T es función porque cada elemento de A tiene imagen única en B.
f) T = {(1,6), (3,4), (5,2), (5,4), (7,6)}
f) T no es función porque 5 є A tiene más de una imagen en B.
g) R = {(3,2), (3,4), (3,6)}
g) R no es función porque hay elementos de A que no tienen imagen y además 3 є A tiene más de una imagen en B.
3) Sean A = {-3,0,3}. Determine si las siguientes relaciones de A en B son o no funciones. Justifique la respuesta.
a) R = {(-3, -3), (0,0), (3, 3)}
b) R = {(0, -3), (3, 0), (-3, 3)}
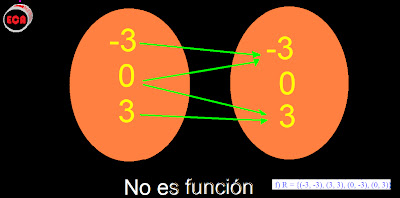
c) R = {(0, -3), (-3, 0), (0, 0)}
d) R = {(-3, 0), (3, 0)}
e) R = {(-3, 0), (0,0), (3, 0)}
f) R = {(-3, -3), (3, 3), (0, -3), (0, 3)}
g) R = {(3, 0), (3, -3), (3, 3)}
a) R = {(-3, -3), (0,0), (3, 3)}
a) R es función porque cada elemento de A imagen única en A.
b) R = {(0, -3), (3, 0), (-3, 3)}
b) R es función porque cada elemento de A tiene una única es A.
- R = {(0, -3), (-3, 0), (0, 0)}
c) R no es función porque 0 є A tiene más de una imagen en A y además hay elementos de A que no tienen imagen.
d) R = {(-3, 0), (3, 0)}
d) R no es función porque 0 no tiene imagen.
e) R = {(-3, 0), (0,0), (3, 0)}
f) R no es función porque 0 є A tiene más de una imagen en A.
g) R = {(3, 0), (3, -3), (3, 3)}
f) R no es función porque 0 є A tiene más de una imagen en A.
g) R = {(3, 0), (3, -3), (3, 3)}
g) R no es función porque hay elementos de A que no tienen imagen en A y además el 3 є A tiene más de una imagen en A.
En un gráfico cartesiano una relación es función si al trazar cualquier paralela al eje y ésta corta en un solo punto al gráfico de la relación.
DEFINICIÓN DE FUNCIÓN:
Sean A y B subconjuntos no vacíos de números reales. Una función f de A en B, es una función que asigna a cada x del conjunto x del conjunto A un único elemento del conjunto B.
Luego se tiene:
f: A --> B
Cada elemento de x Є A se usa la notación f(x) para indicar los elementos de B que ha sido asignado a x.
Al conjunto A se le llama dominio y al conjunto B codominio de la función.
f(x) representa la imagen de x a través de la función dada.
En el plano cartesiano, el conjunto A representa los valores del eje x y el conjunto B los valores en el eje y que han sido asignados a través de la función dada. A partir de esto diremos que f(x) = y.
UNA FUNCIÓN DEL CONJUNTO DE LOS NÚMEROS REALES EN EL CONJUNTO DE LOS NÚMEROS REALES.
Es como una máquina que recibe números reales por la derecha y los entrega por la izquierda. Si la función (o máquina) la denotamos por f y la función transforma a en b. También se dice que b es la imagen de a vía f, en el caso en que la función se subtiende, entonces decimos que b es la imagen de a.
EJERCICIOS RESUELTOS
I .- De acuerdo a la maquina de la figura responde:
a) ¿Qué número saldrá si ingresa un 3?
SOLUCIÓN:
x = 3
x² = 3² = 3 x 3 = 9
b) ¿Qué número saldrá si ingresa un – 4?
x = - 4
x² = (-4)² = (-4)(-4) = 16
c) ¿Qué número debió ingresar a la máquina para que saliera un 9?, ¿ existe otra posibilidad?
X = 3
X² = 3² = 3 x 3 = 9, no existe otra posibilidad. ¿existe otra posibilidad?
X = 0
X² = 0 x 0 = 0 , no existe otra posibilidad.
I.I De acuerdo a la maquina de la figura responde:
a) ¿Qué número saldrá si ingresa un 2?
x = 2
x² + 1 = (2)² + 1 = 5
b) ¿Qué número saldrá si ingresa un -2?
x = -2
x² + 1 = (-2)² + 1 = 5
c) Si finalmente salió un 16 de las máquinas, ¿qué número pudo haber ingresado?, ¿existe otra posibilidad?.
1 + x² = 16 /-1
x² = 16 – 1
x² = 15 / √
x = √15
d) ¿Puede haber salido un – 9 de las máquinas?.¿por qué?
1 + x² = - 9
x² = -9 – 1
x² = (- 10) / √
x = √-10
x = 10i ; no
e) Si sale un 0 finalmente de las máquinas, ¿qué número pudo haber entrado?
1 + x² = 0
x² = 0 – 1
x² = (- 1) / √
x = √- 1
x = -i; no
f) ¿Qué expresión sale de la máquina si ingresa x?
(1 + x² )
I.II Ahora invierte el orden de las máquinas y realiza los problemas anteriores con esta nueva disposición.
a) ¿Qué número saldrá si ingresa un 2?
x = 2
1+ x² = 1+ (2)² = 5
b) ¿Qué número saldrá si ingresa un -2?
x = -2
1 + x² = 1 + (-2)² = 5
c) Si finalmente salió un 16 de las máquinas, ¿qué número pudo haber ingresado?, ¿existe otra posibilidad?.
x² + 1 = 16 /-1
x² = 16 – 1
x² = 15 / √
x = √15
d) ¿Puede haber salido un – 9 de las máquinas?.¿por qué?
1 + x² = - 9
x² = -9 – 1
x² = (- 10) / √
x = √-10
x = 10i ; no
e) Si sale un 0 finalmente de las máquinas, ¿qué número pudo haber entrado?
1 + x² = 0
x² = 0 – 1
x² = (- 1) / √
x = √- 1
x = -i; no
f) ¿Qué expresión sale de la máquina si ingresa x?
(x² + 1)
II Si f: A ---------->; B esta dada por: f(x) = 2x + 1; sabiendo que
A = {1, 2,3} y B = {3, 4, 5, 6,7,8}. ¿Es función? ¿cuáles son las imágenes?
SOLUCIÓN
f(x) = 2x + 1
f(1) = 2(1) + 1 = 3
f(2) = 2(2) + 1 = 5
f(3) = 2(5) + 1 = 7
Por lo tanto, f(x) = 2x + 1, es función, porque todas las imágenes están están en el conjunto B y las imágenes son 3,5, 7.
III.- Si f: R -------> R R = números reales y f(x) = 3x – 2 encuentre:
a) f(- 2) + f (4)
b) f (3) – f(1)
f(2)
SOLUCIÓN
a) f(- 2) + f(4)
f(x) = 3x – 2
f(- 2) = 3 (-2) – 2 = - 8
f(4) = 3 (4) - 2 = 10
Luego f(- 2) + f(4) = - 8 + 10 = 2
b) f (3) – f(1)
f(2)
f(x) = 3x – 2
f(3) = 3(3) – 2 = 7
f(1) = 3(1) – 2 = 1
f(2) = 3(2) – 2 = 4
Luego f (3) – f(1) /f(2) = (7 – 1)/4 = 6/4 = 3/2
IV.- EJERCICIOS PROPUESTOS
- Si f(x) = 3x – 1 es una función de R en R entonces ¿cuál es el valor de f (- 2)?A) 6B) – 6C) 7D) - 7E) 0
SOLUCIÓN
f(x) = 3x – 1
f(- 2) = 3( - 2) – 1 = - 7
- Si f(x) = 3x – 2 una función de R en R determine el valor 2· f(- 1) – f(2) + 5·f(4).A) 50B) – 14C) 36D) - 24E) 20
SOLUCIÓN
f(x) = 3x – 2
f(- 1) = 3(- 1) – 2 = - 5
f(2) = 3(2) – 2 = 4
f(4) = 3(4) – 2 = 10
2· f(- 1) – f(2) + 5·f(4)
2· (- 5) – (4) + 5 (10)
- 10 – 4 + 50 = + 36


























No hay comentarios:
Publicar un comentario