a) R = {(1,4), (2,5), (3,6)}
b) R = {(1,4), (2,4). (3,4)}
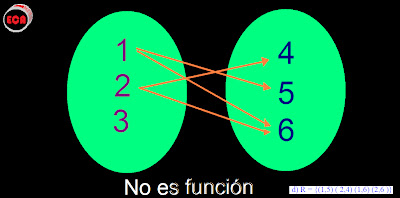
c) R = {(1,4), (1,5), (1,6), (2,4), (3,6)}
d) R = {(1,5), (2,4), (1,6), (2,6)}
e) R = {(1,6), (2,4), (3,6)}
SOLUCIÓN
a) R = {(1,4), (2,5), (3,6)}
a) R es función porque todos los elementos de A tienen una sola imagen en B.
b) R = {(1,4), (2,4), (3,4)}
b) R es función porque todos los elementos de A tienen una sola imagen en B, no importa que ésta sea la misma para todos.
- R = {(1,4), (1,5), (1,6), (2,4), (3,6)}
c) R no es función porque 1 є A tiene más de una imagen en B.
d) R = {(1,5), ( 2,4), (1,6), (2,6 )}
d) R no es función porque 3 є A no tiene imagen en B.
e) R = {(1,6) (2,4) (3,6)}
e) R es función porque todos los elementos de A tienen una única imagen en B.
2) Sean A = {1,3,5,7} y B = {2,4,6}. Determine si las siguientes relaciones de A en B son o no funciones. Justifique la respuesta.
a) R = {(1,2), (3,4), (5,6), (7,6)}
b) R = {(1,2), (3,4), (5,6)}
c) S = {(3,4), (5,6), (7,2), (7,4)}
d) S = {(1,4), ( 3,4), (5,4), (7,4 )}
e) T = {(7,6), (5,4), (3,2), (1,2)}
f) T = {(1,6), (3,4), (5,2), (5,4), (7,6)}
g) R = {(3,2), (3,4), (3,6)}
SOLUCIÓN
a) R = {(1,2), (3,4), (5,6), (7,6)}
a) R es función porque cada elemento de A tiene imagen única en B.
b) R = {(1,2), (3,4), (5,6)}
b) R no es función porque 7 є A no tiene imagen en B.
c) S = {(3,4), (5,6), (7,2), (7,4)}
c) S no es función porque 1 є A no tiene imagen en B y además 7 є A tiene más de una imagen.
d) S = {(1,4), ( 3,4), (5,4), (7,4 )}
d) S es función porque cada elemento de A tiene imagen única en B.
e) T = {(7,6), (5,4), (3,2), (1,2)}
e) T es función porque cada elemento de A tiene imagen única en B.
f) T = {(1,6), (3,4), (5,2), (5,4), (7,6)}
f) T no es función porque 5 є A tiene más de una imagen en B.
g) R = {(3,2), (3,4), (3,6)}
g) R no es función porque hay elementos de A que no tienen imagen y además 3 є A tiene más de una imagen en B.
3) Sean A = {-3,0,3}. Determine si las siguientes relaciones de A en B son o no funciones. Justifique la respuesta.
a) R = {(-3, -3), (0,0), (3, 3)}
b) R = {(0, -3), (3, 0), (-3, 3)}
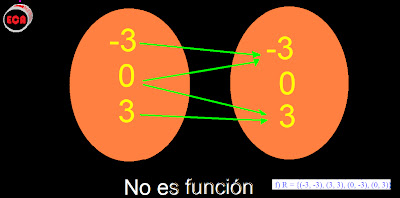
c) R = {(0, -3), (-3, 0), (0, 0)}
d) R = {(-3, 0), (3, 0)}
e) R = {(-3, 0), (0,0), (3, 0)}
f) R = {(-3, -3), (3, 3), (0, -3), (0, 3)}
g) R = {(3, 0), (3, -3), (3, 3)}
a) R = {(-3, -3), (0,0), (3, 3)}
a) R es función porque cada elemento de A imagen única en A.
b) R = {(0, -3), (3, 0), (-3, 3)}
b) R es función porque cada elemento de A tiene una única es A.
- R = {(0, -3), (-3, 0), (0, 0)}
c) R no es función porque 0 є A tiene más de una imagen en A y además hay elementos de A que no tienen imagen.
d) R = {(-3, 0), (3, 0)}
d) R no es función porque 0 no tiene imagen.
e) R = {(-3, 0), (0,0), (3, 0)}
f) R no es función porque 0 є A tiene más de una imagen en A.
g) R = {(3, 0), (3, -3), (3, 3)}
f) R no es función porque 0 є A tiene más de una imagen en A.
g) R = {(3, 0), (3, -3), (3, 3)}
g) R no es función porque hay elementos de A que no tienen imagen en A y además el 3 є A tiene más de una imagen en A.


















No hay comentarios:
Publicar un comentario