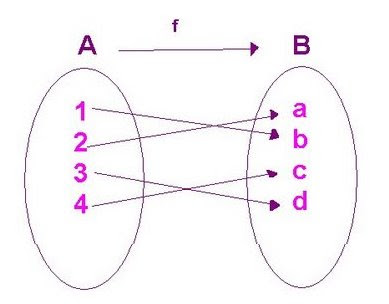
Una función f: A -> B es biyectiva si y solo si es 1 - 1 y sobre.
A cada elemento de A le corresponde un único elemento de B.
De los siguientes ejemplos .¿Cuál(es) es(son) función(es) epiyectiva o sobre.
A cada elemento de A le corresponde un único elemento de B.
De los siguientes ejemplos .¿Cuál(es) es(son) función(es) epiyectiva o sobre.
SOLUCIÓN
a) f1 no es biyectiva porque no es uno a uno ni sobre.
b) f2 no es biyectiva porque no es uno a uno.
C) f3 no es biyectiva porque no es sobre.
d) f4 es biyectiva porque es uno a uno y sobre.
Una función f: A ->;B se dice biyectiva si y sólo si es uno a uno y sobre.
a) f1 no es biyectiva porque no es uno a uno ni sobre.
b) f2 no es biyectiva porque no es uno a uno.
C) f3 no es biyectiva porque no es sobre.
d) f4 es biyectiva porque es uno a uno y sobre.
Una función f: A ->;B se dice biyectiva si y sólo si es uno a uno y sobre.
FUNCIÓN EPIYECTIVA O SOBRE
Una función f: A-->B se dice epiyectiva o sobre si y sólo si todo elemento de B es imagen de algún elemento de A
( f: A --> B es sobre ) <=> ( Rang f = B)
Veamos un ejemplo:
Todo elemento de A debe tener a lo menos una imagen en B
De los siguientes ejemplos .¿Cuál(es) es(son) función(es) epiyectiva o sobre.
SOLUCIÓN
a) f1 no es sobre porque 6 no pertenece al Rang de f1.
b) f2 es epiyectiva o sobre porque el Rang de f2 = B.
C) f3 no es sobre porque 6 no pertenece al Rang de f3 = {5,6,7} es diferente a B = {5,6,7,8}
d) f4 es sobre porque el Rang de f4 = {5,6,7,8} = B
Una función f: A-->B se dice epiyectiva o sobre si y sólo si todo elemento de B es imagen de algún elemento de A
a) f1 no es sobre porque 6 no pertenece al Rang de f1.
b) f2 es epiyectiva o sobre porque el Rang de f2 = B.
C) f3 no es sobre porque 6 no pertenece al Rang de f3 = {5,6,7} es diferente a B = {5,6,7,8}
d) f4 es sobre porque el Rang de f4 = {5,6,7,8} = B
Una función f: A-->B se dice epiyectiva o sobre si y sólo si todo elemento de B es imagen de algún elemento de A
( f: A -> ; B es sobre ) <=> ( Rang f = B)
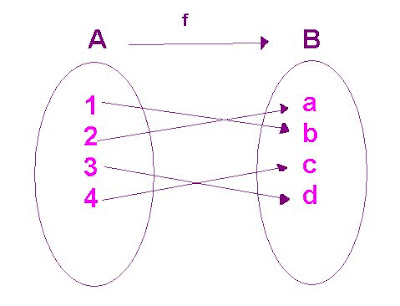
Una función f: A-> B se dice inyectiva o uno a uno si y sólo si elementos distintos en A le corresponden imágenes distintas en B.
Veamos un ejemplo:
f es uno a uno, porque imágenes distintas corresponden a pre- imágenes distintas.
De los siguientes ejemplos .¿Cuáles es(son) función(es) inyectiva o uno a uno?
SOLUCIÓN:
a) No es función inyectiva o uno a uno porque a 7 es imagen de dos elementos distintos, el 2 y el 3.
b) No es función inyectiva o uno a uno ya que f2(3) = 7 y f2(4) = 7 3 es distinto a 4.
c) Es función inyectiva o uno a uno porque imágenes distintas le corresponden pre-imágenes distintas.
d) Es función inyectiva o uno a uno. Porque a cada imagen le corresponde una pre- imagen distinta.
No hay comentarios:
Publicar un comentario